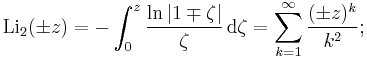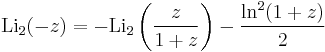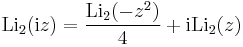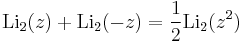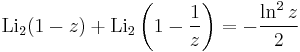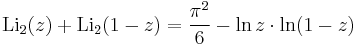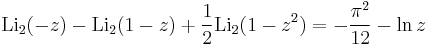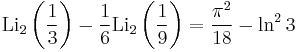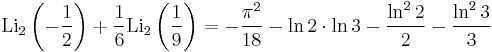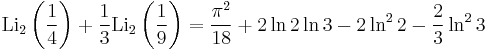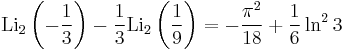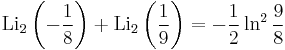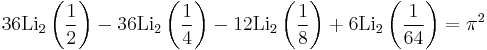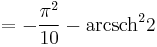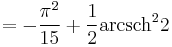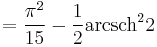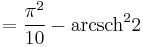Spence's function
See also: polylogarithm#Dilogarithm
In mathematics, Spence's function, or dilogarithm, denoted as Li2(z), is a particular case of the polylogarithm. Lobachevsky's function and Clausen's function are closely related functions. Two related special functions are referred to as Spence's function, the dilogarithm itself, and its reflection with the variable negated:
William Spence, after whom the function was named by early writers in the field, was a Scottish mathematician working in the early nineteenth century.[1] He was at school with John Galt,[2] who later wrote a biographical essay on Spence.
Contents |
Identities
Special values
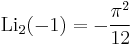 A072691
A072691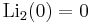
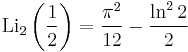 A076788
A076788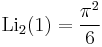 A013661
A013661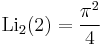 A091476
A091476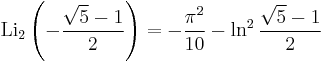
-
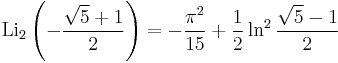 A152115
A152115
-
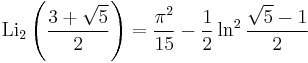
-
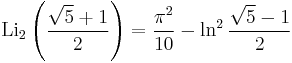
-
References
- Lewin, L. (1958), Dilogarithms and associated functions, Foreword by J. C. P. Miller, Macdonald, London, MR0105524
- Morris, Robert (1979). "The dilogarithm function of a real argument". Math. Comp. 33 (146): 778-787. doi:10.1090/S0025-5718-1979-0521291-X. MR521291.
- Kirillov, Anatol N. (1994). "Dilogarithm identities". arXiv:hep-th/9408113.
- Osacar, Carlos; Palacian, Jesus; Palacios, Manuel (1995). "Numerical evaluation of the dilogarithm of complex argument". Celestial Mech. Dynam. Astron. 62 (1): 93-98. doi:10.1007/BF00692071.
- Zagier, Don. "The Dilogarithm Function". http://maths.dur.ac.uk/~dma0hg/dilog.pdf.
- Zagier, Don (2007). "The Dilogarithm Function". Front. Number Theory, Physics, Geom. II: 3-65. doi:10.1007/978-3-540-30308-4_1.